| Funding agency | Austrian Science Fund (FWF) |
|---|---|
| Project number | Y 192 |
| Principal investigator | Joachim Schöberl |
| Duration | 2002-08-01 – 2008-12-31 |
Mechanical deformations, magnetic fields, and many other applications from science and engineering are mathematically described by partial differential equations. The finite element method (fem) is certainly the most powerful tool for the computer simulation of such models. Here, the object under investigation is decomposed in many small elements such as triangles, quadrilaterals or tetrahedra. Fig 1 shows such a finite element mesh of a crank shaft. These elements are used for the representation of field functions such as the mechanical deformation or the magnetic flux. One possibility is to choose the function value in each vertex of the mesh, and then use linear interpolation on the elements. These gives a description of the problem, but, to obtain the solution, a large system of equations has to be solved. The result, i.e., the field function, can be visualized, and representative quantities can be computed. Fig 2 shows the internal stresses of the crank shaft.
Fig. 1
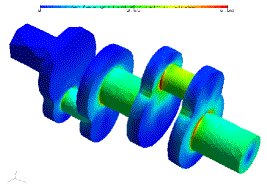
Fig. 2
Due to rapidly growing computing performance, more and more complicated models can be solved more and more accurately. One observes that the larger the problem, the more important are efficient algorithms. For the finite element method two aspects play an essential role. First, an efficient distribution of elements is crucial. In critical regions, many small elements shall be used, while other regions may be covered by just a few, large elements. The objective is an automatic strategy for an adaptive distribution of elements. The second point is the equation solver. For conventional solvers such as Gaussian elimination, the required computing time grows more than proportional to the problem size. On the other hand, modern iterative solvers are often much faster. Here, one can obtain a proportional relation between problem size and computing time.
One version of the fem is the so called h-version. Here, the accuracy is controlled by the number of elements. For example, the stress field in Fig 2 is computed by using 2 million unknowns. A different version of the fem, the p-version, operates on a fixed mesh, and increases the number of parameters per element. The advantage of the second method is that smooth functions can be approximated very well by high order polynomials. On the other hand, local effects such as stress singularities in the notches are captured more efficiently on fine meshes. The hp-version combines the advantages of both methods. Both, the mesh size and the polynomial degree are varied. This results in an extremely (exponentially) fast convergence.
While two dimensional problems can be solved with hp-fem, three dimensional problems are still a big challenge. Here, fast solvers as well as automatic mesh control are hot topics in research. The principal investigator is experienced in theory as well as implementation of the h-version of the fem. The goal of this START project is an essential contribution to the theory of the hp-fem, as well as the development of software for the computer simulation of real life problems.