| Title | All-at-once Multigrid Methods for Optimality Systems Arising from Optimal Control Problems |
|---|---|
| Author | Stefan Takacs |
| Funding | FWF Doctoral Program "Computational Mathematics" (W1214), Subproject DK 12 - Robust solvers for KKT systems (lead by W. Zulehner) |
| Institution | Johannes Kepler University Linz |
| Supervisor | Walter Zulehner |
| External reviewer | Andrew Wathen (University of Oxford, UK) |
In this thesis we construct and analyze multigrid methods for solving the optimality system characterizing the solution of an optimal control problem. Originally multigrid methods were constructed for elliptic problems. However, the (discretized) optimality system is not elliptic. We make use of the fact that the matrix is a block-matrix with saddle point structure: on the one hand we have two blocks of variables representing state and control. These two blocks are already part of the optimal control problem itself. On the other hand, the conversion to the optimality system requires the introduction of Lagrange multipliers, which form the third block of variables.
There are several possibilities to use multigrid methods for constructing solvers for such saddle point problems. One approach to solve such problems is to apply multigrid methods in every step of an overall block-structured iterative method to equations in just one of these blocks of variables. Another approach, which we will follow here, is to apply the multigrid idea directly to the (reduced or not reduced) optimality system, which is called an all-at-once approach.
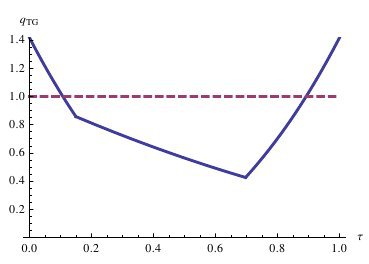
The choice of an appropriate smoother is the key issue in constructing such a multigrid method. The other part of the method—the coarse-grid correction—can be set up in a canonical way because we will use a framework of conforming geometric multigrid method. In this framework the smoother will be constructed such that the convergence rates are independent of the grid level. This leads to an overall computational complexity that is linear in the number of unknowns which is called an optimal convergence.
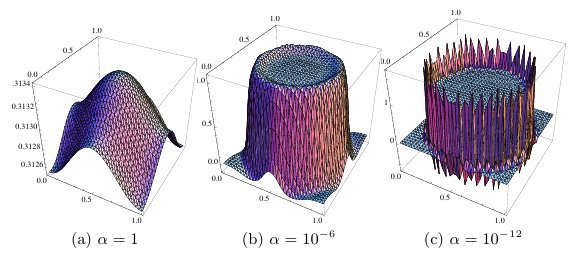
For a sub-class of the class of problems we will introduce in a first point, we will go one step further and construct methods where the convergence rates are also robust in a certain regularization or cost parameter which is part of the problem. Moreover, we will show this fact. Methods that do not take this into account typically show quite poor convergence rates if this parameter attains small values. For the analysis, we will introduce a general framework that is based on Hackbusch's splitting of the analysis into smoothing and approximation property. This allows to give general convergence theorems for the methods under investigation. A second point we consider is local Fourier analysis which allows to compute sharp bounds of the convergence rates.