| Funding agency | Austrian Science Fund (FWF) |
|---|---|
| Project number | P 29181 |
| Principal investigator | Urlich Langer |
| International Research Partner and Co-Investigator | Thomas Wick |
| International Research Partners | Ira Neitzel Winnifred Wollner |
| PhD Students | Bernhard Endtmayer Daniel Jodlbauer |
| Duration | 2017-08-01 – 2020-07-31 |
This website documents the work in the project Goal-Oriented Error Control for Phase-Field Fracture Coupled to Multiphysics Problems, which is supported by the Austrian Science Fund (FWF) under grant P29181-N31. This is a joint project of the Johann Radon Institute for Computational and Applied Mathematics (RICAM) of Austrian Academy of Sciences in Linz, the Institute of Computational Mathematics at the Johannes Kepler University in Linz and the Institute of Applied Mathematics Hannover (IfAM) in Germany.
In many applications the accurate evaluation of certain goal functionals is the key subject of interest. In this project this aim will be addressed for quantities of interest in phase-field fracture propagation and its coupling to multiphysics problems and optimization. The basic fracture model in elasticity is based on a variational formulation of Griffith's brittle fracture approach. The resulting Euler-Lagrange system consists of two coupled partial differential equations and is subject to a crack irreversibility constraint, which leads to a variational inequality. Currently, variational models for fracture (and also damage) have gained high interest in applied mathematics and engineering. However, even the most basic approach (treating cracks in linearized elasticity) is challenging due to non-convexity of the underlying energy functional and the interplay of certain model and discretization parameters. The latter aspect is worth to be mentioned since these parameters influence the robustness and efficiency of solvers and more importantly for this project, they may have significant influence on the accuracy and convergence order of goal functionals such as crack path, crack opening displacements, displacement point values, evaluation of stresses or global norms of displacements or the phase-field variable. An efficient method for goal-functional evaluations and local mesh adaptivity is the so-called dual-weighted residual (DWR) method. Here, a (linear) adjoint problem delivers weights for the a posteriori error estimator. It is of immediate importance for further verification to continue to develop error control for the basic model of phase-field fracture in linearized elasticity as well as its integration in multiphysics and optimization problems. Consequently, computational and numerical analysis of phase-field fracture for cracks in elasticity comprise the first part of this proposal. This requires careful techniques since fracture propagation is time-dependent (or quasi-stationary) and a variational inequality.
The second goal is the application of the DWR method to phase-field fracture optimal control problems. In particular this goal is innovative and allows to unlock new research fields and algorithmic techniques associated with fracture mechanics. This second part is planned in close collaboration with Prof. Ira Neitzel (Bonn/Germany) and Prof. Winnifried Wollner (Darmstadt/Germany). The third aspect comprises DWR error control for a coupled (quasi-stationary) phase-field-fluid-structure interaction problem. In this third part an international interdisciplinary collaboration with Dr. Jeremi Mizerski (medical doctor in Warsaw/Poland) with regard to mathematical modeling and discussions of relevant quantities of interest is planned. Here, the treatment of multiple goal functionals simultaneously (e.g., drag and crack opening displacement) is of high relevance. A success of this project would allow for future extensions to other practical field problems such as fluid-filled fracture propagation in porous media or hemodynamics.
Local error distribution in multi goal oriented adaptivity.
Multigoal-Oriented Error Estimates for Non-linear Problems [doi] [preprint]
Resulting mesh using local adaptivity.
Multigoal-Oriented Error Estimates for Non-linear Problems [doi] [preprint]
Diagonal tearing of a simplified 2d screw.
Fracture propagation in a 3d L-shaped panel due to cyclic loading on the right edge.
Matrix-free multigrid solvers for phase-field fracture problems [report] [arXiv]
Fracture propagation in a 2d L-shaped panel due to cyclic loading on the right edge.
Matrix-free multigrid solvers for phase-field fracture problems [report] [arXiv]
Final crack pattern for the multiple fracture test case.
Matrix-free multigrid solvers for phase-field fracture problems [report] [arXiv]
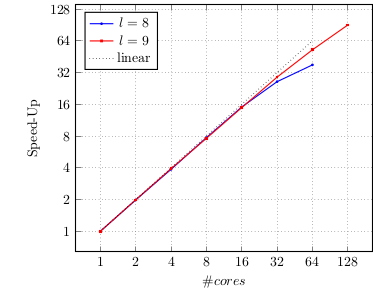
Parallel scalability of the matrix-free multigrid solver for the multiple fracture test.
Matrix-free multigrid solvers for phase-field fracture problems [report] [arXiv]
We enjoy discussions with